Matière

Protomatière, seuils et transions

Si l’espace-temps se déploie dans un hyper-volume à six dimensions, il semble que ce ne soit pas la limite de l’extension de CELA. Lorsqu’une pression interne devient trop élevée, dépassant la capacité des spations à la contenir dans les six axes, une rupture de confinement pourrait survenir.

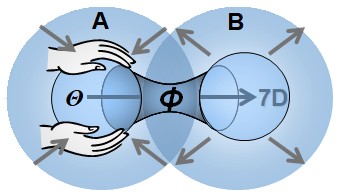
Lorsque la pression locale dans un spation dépasse sa limite maximale de cohérence, sa structure interne ne peut plus se maintenir dans la configuration à six axes qui définit l’espace-temps ordinaire. Dans cette situation, un des six axes est substitué par l’axe 7, donnant naissance à une configuration à sept axes. Cette transformation ne déplace pas le spation : elle modifie sa structure interne. Le spation ainsi réarrangé n’appartient plus à l’espace-temps 6D, car il ne respecte plus les règles de connexion qui rendent l’espace-temps continu et observable. Il devient alors invisible depuis notre domaine, bien qu’il continue d’exister dans une structure 7D plus compacte et plus dense. Ce phénomène n’est pas une transition progressive, mais un seuil : dès que la configuration 6D cesse d’être stable, l’axe 7 est immédiatement sélectionné.

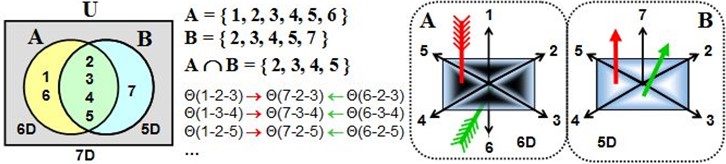
Cette représentation est volontairement simplifiée. Lorsque l’axe 7 intervient, la structure qui en résulte n’est plus décrite par les combinaisons habituelles des six axes de l’espace-temps. Dans ce nouveau domaine, certaines configurations supplémentaires deviennent possibles, mais elles ne sont pas accessibles depuis l’espace-temps 6D. Nous appelons ce second domaine B pour distinguer l’espace-temps ordinaire (domaine A) de la région où l’axe 7 est actif. Dans cette page, nous continuerons à nous concentrer exclusivement sur les phénomènes se produisant en A.

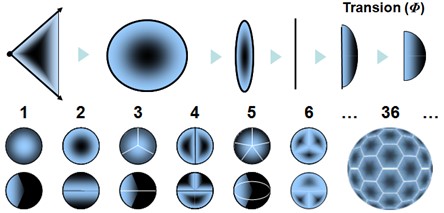
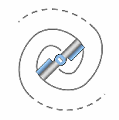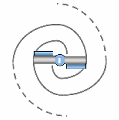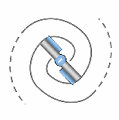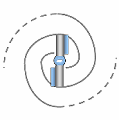
Compte tenu de la pression très élevée qui règne dans l’espace-temps, lorsqu’un spation dépasse sa limite de cohérence et bascule en configuration 7D, il cesse immédiatement d’appartenir au domaine 6D. Le point précis où ce basculement se produit est appelé transion. Un transion n’est pas un « trou » et n’implique pas encore d’écoulement ou de déplacement collectif. Il s’agit simplement de l’endroit où un spation perd sa structure à six axes et adopte la structure à sept axes, devenant ainsi invisible au domaine 6D. Dans les illustrations qui suivent, nous représentons un transion par un petit cercle au centre des schémas, pour indiquer l’endroit où s’opère ce changement de domaine.

Lorsqu’un transion se maintient dans l’espace-temps, il n’agit plus seulement sur le spation qui a franchi sa limite : il provoque un afflux des spations environnants vers son centre. Sous l’effet de la pression colossale du milieu, les spations voisins sont progressivement entraînés vers le transion.

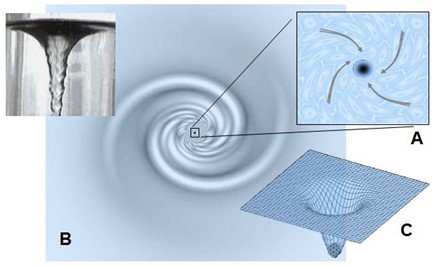
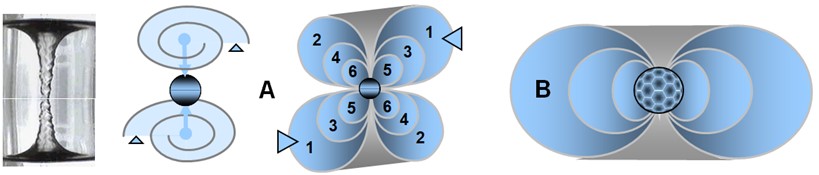
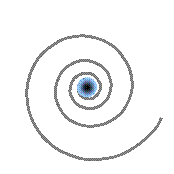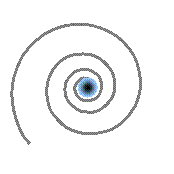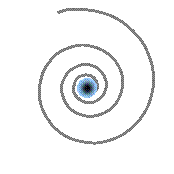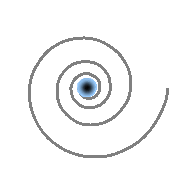
Comme illustré en (A), ce déplacement ne s’effectue pas en ligne droite : la viscosité du champ spationique leur impose une rotation. Les spations se mettent alors à tourner en spirale autour du transion, formant un vortex stable.

La figure (B) donne une analogie classique : celle d’un vortex dans un liquide, capturant visuellement la dynamique de chute structurée. Mais contrairement à un fluide ordinaire, ce vortex ne « tombe » pas vers un centre matériel : le mouvement suit une orientation dimensionnelle induite par le transion.

En (C), la pression locale diminue vers le cœur du vortex. L’énergie de pression se convertit en énergie cinétique. Cette baisse de pression renforce l’aspiration, ce qui entretient l’écoulement spiralé : le vortex s’auto-alimente.

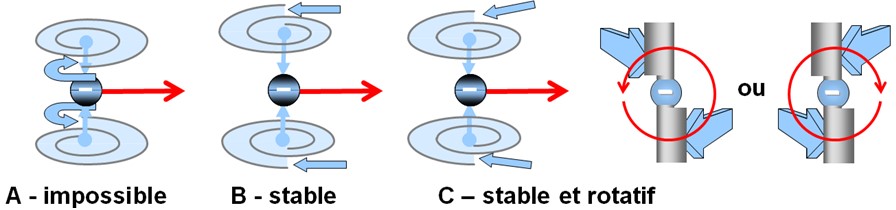
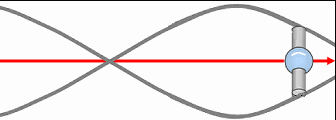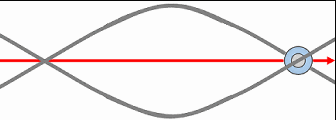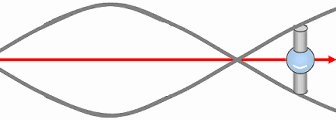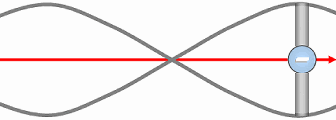
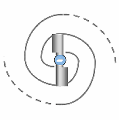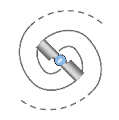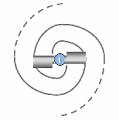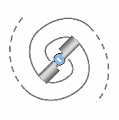
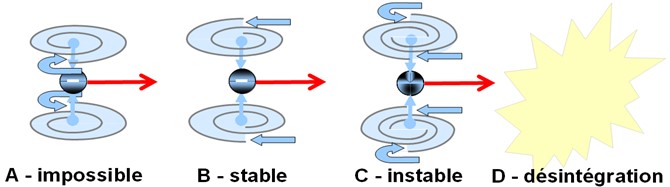
Lorsque le transion entraîne un nombre pair de spations simultanément, l’écoulement se divise en deux vortex conjugués, comme illustré en (A). Ces vortex tournent en sens inverse et se stabilisent l’un par l’autre. Cette structure reste possible tant que le nombre de spations transférés reste faible. Cependant, lorsque le nombre de spations entraînés simultanément augmente, la synchronisation des deux vortex devient de plus en plus difficile : la moindre fluctuation de pression déséquilibre la configuration et tend à la faire s’écrouler. Dans ce régime, la configuration se réorganise spontanément en un vortex unique, comme illustré en (B). Cette structure unipolaire devient alors plus stable, plus cohérente et plus probable que la configuration bipolaire. Ce basculement de la stabilité jouera un rôle essentiel dans l’émergence de la charge et des familles de particules, étudiées dans l’image suivante.

Fermions, vortex, chiralité et charge

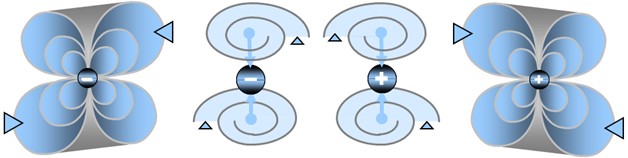
Toute particule de type fermion — c’est-à-dire toute particule dotée d’une masse stable — possède une circulation interne du champ spationique organisée en vortex. Ce mouvement interne n’est pas aléatoire : il s’enroule selon une spirale. Cette spirale peut tourner dans l’un ou l’autre sens. On appelle cela la chiralité :

• s = -1 : le vortex tourne dans un sens
• s = +1 : le vortex tourne dans le sens opposé

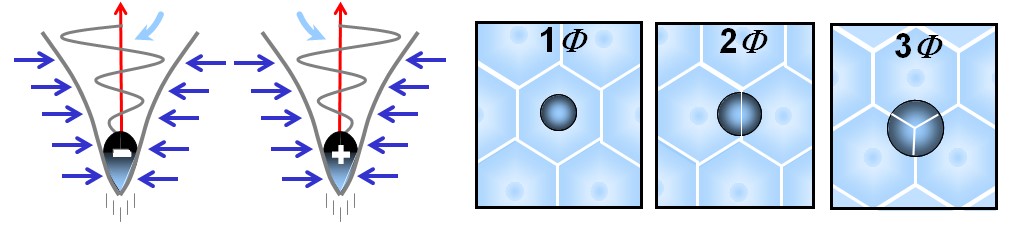
La chiralité ne change pas la forme de la particule, mais elle détermine le signe de sa charge électrique. Autrement dit, ce n’est pas la particule qui change, mais la direction de son vortex interne. Ainsi, une particule et son antiparticule sont identiques dans leur structure, mais leur vortex tourne en sens opposé. C’est cette différence d’orientation qui explique pourquoi l’une porte une charge positive et l’autre une charge négative.

Spin, rotation interne du vortex

Tout fermion possède un mouvement de rotation interne appelé spin. Ce mouvement ne correspond pas à une rotation de la particule dans l’espace, mais à la rotation du vortex interne qui la constitue. Dans ce vortex, les spations tournent en spirale autour du centre, et l’ensemble du vortex peut lui-même tourner légèrement en avance ou en retard par rapport au flux global. Ce mouvement interne donne naissance à un moment cinétique intrinsèque, c’est-à-dire une propriété de rotation qui existe même si la particule est immobile.

Comme la chiralité, le spin peut prendre deux orientations possibles, ce qui sera observé dans les expériences comme « spin vers le haut » ou « spin vers le bas ». Cependant, ces deux orientations ne changent ni la masse ni la structure de la particule : elles représentent simplement deux états d’équilibre possibles de son vortex interne.

Onde Statique Associée

La rotation interne d’un fermion, comme l’électron, ne reste pas confinée en son centre. Elle laisse dans l’espace-temps qui l’entoure une empreinte stable, sous la forme d’une onde statique. Il ne s’agit pas d’une onde qui se propage, mais d’une structure immobile liée à la présence et à l’orientation du vortex interne. Cette onde agit comme un champ directionnel autour de la particule : elle indique dans quel sens son vortex tourne et permet ainsi à la particule de s’orienter ou de s’aligner, par exemple dans un champ magnétique. La taille de cette onde dépend de la vitesse de la particule. Plus la particule se déplace vite, plus son vortex interne se resserre, et plus l’onde statique qui l’accompagne devient courte. À l’inverse, lorsqu’elle se déplace lentement, le vortex est plus large et l’onde statique plus étendue. Cette onde statique joue donc le rôle de mémoire du spin en mouvement : elle accompagne la particule et conserve l’orientation de son vortex interne tout au long de son déplacement.

Neutrino, vortex ouvert et neutralité

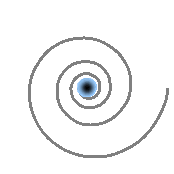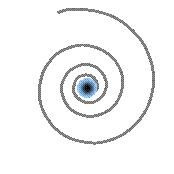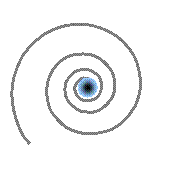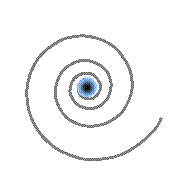
Toutes les particules ne possèdent pas la même structure interne. Certaines, comme l’électron, sont constituées d’un vortex fermé et bien ancré dans l’espace-temps. D’autres, comme le neutrino, sont formées d’un vortex ouvert, beaucoup plus léger. Dans ce modèle, le neutrino correspond à la forme la plus simple possible du vortex : un tourbillon unique, sans charge électrique. Comme il n’interagit pas avec les champs électromagnétiques, il traverse la matière presque sans effet, ce qui explique pourquoi il est si difficile à détecter.

Le neutrino possède néanmoins un spin (une orientation interne de rotation), mais celle-ci est toujours la même : elle ne peut pas être inversée par interaction électromagnétique. Cela le distingue des particules chargées, dont la rotation peut être retournée par un champ. Sa masse est extrêmement faible. Cela s’explique naturellement ici : un vortex ouvert est beaucoup moins compact qu’un vortex fermé, et comporte donc beaucoup moins d’énergie. Cette géométrie conduit à une masse très faible, conforme aux valeurs mesurées en laboratoire.

Générations de Particules

Toutes les particules d’une même famille (comme l’électron, le muon et le tau) possèdent la même structure interne de vortex. La différence entre elles ne vient pas de leur forme, mais de leur degré de compacité : à quel point le vortex est resserré sur lui-même. Lorsqu’un vortex est faiblement compact, la particule est légère et stable. S’il est plus resserré, la densité interne augmente, ce qui rend la particule plus massive et moins stable. Et lorsque le vortex est extrêmement compact, la particule devient très lourde et ne se maintient que brièvement. C’est ainsi que le modèle explique naturellement l’existence des trois générations de particules :

• 1ère génération : vortex peu compact → léger, stable, fréquent (ex : électron, quark up)
• 2e génération : vortex plus compact → plus lourd, moins stable (ex : muon, quark charm)
• 3e génération : vortex très compact → très lourd, instable (ex : tau, quark top)

Cette hiérarchie ne résulte pas de propriétés arbitraires : elle découle directement de la géométrie du vortex interne et de la manière dont il interagit avec la pression de l’espace-temps. En d’autres termes, la masse d’une particule n’est pas « ajoutée » de l’extérieur : elle est la conséquence de la compacité de son vortex interne.

Saveurs Dimensionelles

Chaque particule n’est pas seulement définie par sa masse ou sa charge : elle possède aussi une saveur dimensionnelle. Ce terme désigne la manière dont son vortex interne est organisé dans l’espace-temps. Par exemple, l’électron appartient à la saveur 1-2-3 (dite saveur électron) : son vortex utilise cette organisation spatiale particulière. Le neutrino, lui, est de saveur 4-5-6 (dite saveur neutrino), dans laquelle le vortex est orienté différemment. Toutes les particules partageant un ou plusieurs axes avec la saveur électron peuvent porter une charge électrique. Au contraire, celles fondées sur la saveur neutrino ne partagent aucun axe avec la saveur électron, et n’ont pas de charge électrique.

Certaines particules peuvent partager en partie la même saveur que l’électron. Dans ce cas, leur charge apparaît fractionnaire (comme 2/3 ou 1/3), ce qui est exactement ce que l’on observe pour les quarks. Ainsi, la charge électrique découle simplement du degré de similitude entre leur vortex interne et celui de l’électron. Autrement dit, la saveur dimensionnelle détermine quelles particules peuvent interagir avec l’électron et lesquelles ne le peuvent pas. Cette notion jouera un rôle central dans la compréhension des forces fondamentales que nous aborderons dans la section suivante.

Pour aller plus loin

Cette présentation vulgarisée s’appuie sur un corpus technique formalisé de plus de 255 documents. Pour examiner les fondements rigoureux du modèle CdR :

• image030 — Seuil de Transion — Limite structurelle du spation
• image031 — Intersection combinatoire — Passage 6D → 7D
• image032 — Grammaire visuelle des transions — Représentations 6D → 7D
• image033 — Transion actif — vortex d’écoulement réel à spirale d’entrée
• image034 — Dynamique post-transion — double-vortex Φ et bascule unipolaire
• image035 — Vortex 6D — première structure matérielle stable
• image036 — Modes internes de rotation — spin comme mode interne des vortex Φ
• image037 — Stabilité interne du double-vortex — déphasage de spin quantifié
• image038 — Onde statique intrinsèque — mode n et structure spatiale
• image039 — Origine interne de la masse — énergie de configuration et compacité du champ Φ
• image040 — Générations de particules — compacité interne 1Φ, 2Φ et 3Φ
• image041 — Limite de compacité interne — transition du vortex vers l’instabilité
• image042 — Table complète des particules — Cohérence du vortex Φ et masses émergentes

Ces documents détaillent la dérivation géométrique des particules de matière à partir du champ Φ (seuils de pression, hystérésis de compacité, charges, spin, masses et générations), ainsi que les simulations numériques et critères de falsifiabilité associés.